В геометрии вопрос о сумме диагонали квадрата требует уточнения, так как может пониматься в разных смыслах. Рассмотрим основные интерпретации этого вопроса.
Содержание
Основные трактовки понятия "сумма диагонали"
| Интерпретация | Объяснение |
| Длина диагонали | Геометрическая протяженность диагонали квадрата |
| Сумма длин обеих диагоналей | Общая длина двух диагоналей квадрата |
| Сумма элементов на диагонали | Для квадратных матриц и таблиц |
Длина диагонали квадрата
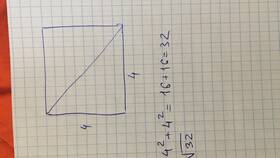
Для квадрата со стороной a длина диагонали d вычисляется по формуле:
- d = a√2
- Это следует из теоремы Пифагора
- Пример: при a = 1, d ≈ 1.4142
Сумма длин обеих диагоналей
Поскольку у квадрата две равные диагонали:
- Длина одной диагонали: d = a√2
- Сумма длин двух диагоналей: 2d = 2a√2
- Пример: при a = 1, сумма ≈ 2.8284
Пример расчета для квадрата со стороной 5 см
| Параметр | Расчет | Результат |
| Длина одной диагонали | 5 × √2 | ≈ 7.071 см |
| Сумма длин двух диагоналей | 2 × 5 × √2 | ≈ 14.142 см |
Сумма элементов на диагонали матрицы
Для квадратной матрицы размером n×n:
- Главная диагональ: элементы aii (где i = 1,2,...,n)
- Сумма диагональных элементов: Σaii
- Пример: для матрицы [[1,2],[3,4]] сумма равна 1 + 4 = 5
Свойства диагоналей квадрата
| Свойство | Описание |
| Равная длина | Обе диагонали одинаковы по длине |
| Перпендикулярность | Диагонали пересекаются под прямым углом |
| Точка пересечения | Делят друг друга пополам |
Таким образом, ответ на вопрос о сумме диагонали квадрата зависит от конкретной постановки задачи. В геометрическом контексте обычно рассматривают длину одной диагонали или сумму длин обеих диагоналей, которые вычисляются через длину стороны квадрата с использованием квадратного корня из двух.