Тангенс суммы двух углов - это важная тригонометрическая формула, позволяющая выразить тангенс суммы через тангенсы отдельных углов. Рассмотрим ее вывод и применение.
Содержание
Формула тангенса суммы
Для любых двух углов α и β (где cos(α+β) ≠ 0 и cosα·cosβ ≠ 0) справедлива формула:
tan(α + β) = (tanα + tanβ) / (1 - tanα·tanβ)
Вывод формулы
- Используем определение тангенса: tan(α+β) = sin(α+β)/cos(α+β)
- Применяем формулы синуса и косинуса суммы:
- sin(α+β) = sinα·cosβ + cosα·sinβ
- cos(α+β) = cosα·cosβ - sinα·sinβ
- Делим числитель и знаменатель на cosα·cosβ
- Получаем искомую формулу
Примеры применения
| Углы | Вычисление |
| tan(30° + 45°) | (tan30° + tan45°)/(1 - tan30°·tan45°) = (√3/3 + 1)/(1 - √3/3·1) ≈ -3.732 |
| tan(π/4 + π/6) | (1 + √3/3)/(1 - 1·√3/3) ≈ 3.732 |
Частные случаи
- При α = β: tan(2α) = 2tanα/(1 - tan²α) - формула двойного угла
- При tanα·tanβ = 1: тангенс суммы не существует (знаменатель обращается в ноль)
- Для малых углов: tan(α+β) ≈ α + β (если углы в радианах)
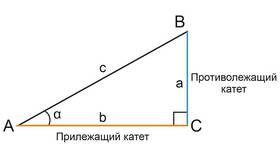
Геометрическая интерпретация
Формулу можно представить через соотношение сторон прямоугольного треугольника, где:
- tanα и tanβ - тангенсы составляющих углов
- tan(α+β) - тангенс результирующего угла
Применение в задачах
- Упрощение тригонометрических выражений
- Решение уравнений
- Доказательство тождеств
- Вычисление точных значений тригонометрических функций
| Задача | Решение с использованием формулы |
| Вычислить tan75° | tan(45°+30°) = (1 + √3/3)/(1 - 1·√3/3) = 2 + √3 |
Формула тангенса суммы является мощным инструментом в тригонометрии и находит применение в различных разделах математики, физики и инженерных расчетов.