Сумма внутренних углов выпуклого n-угольника является важной характеристикой в геометрии, позволяющей решать разнообразные задачи на вычисление углов многоугольников. Данная формула выводится из свойства суммы углов треугольника.
Содержание
Основная формула
Для любого выпуклого n-угольника сумма внутренних углов вычисляется по формуле:
S = (n - 2) × 180°
где n - количество сторон (и углов) многоугольника.
Доказательство формулы
Формула выводится следующим образом:
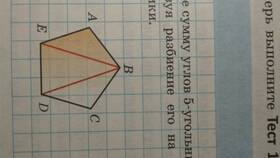
- Выпуклый n-угольник можно разбить на (n - 2) треугольника, проведя диагонали из одной вершины
- Сумма углов каждого треугольника равна 180°
- Общая сумма углов многоугольника равна сумме углов всех полученных треугольников
- Следовательно, S = (n - 2) × 180°
Примеры вычислений
| Многоугольник | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | (3-2)×180° = 180° |
| Четырехугольник | 4 | (4-2)×180° = 360° |
| Пятиугольник | 5 | (5-2)×180° = 540° |
| Шестиугольник | 6 | (6-2)×180° = 720° |
Сумма внешних углов
Для любого выпуклого n-угольника сумма внешних углов, взятых по одному при каждой вершине, всегда равна 360°, независимо от количества сторон:
Σ внешних углов = 360°
Применение формулы
Зная сумму углов n-угольника, можно:
- Находить неизвестные углы правильного многоугольника
- Определять количество сторон многоугольника по известной сумме углов
- Решать задачи на построение многоугольников
- Проверять возможность существования многоугольника с заданными углами
Особые случаи
Для правильных многоугольников (с равными сторонами и углами):
- Каждый внутренний угол = (n-2)×180°/n
- Каждый внешний угол = 360°/n
- Внутренний и внешний углы в сумме дают 180°
Заключение
Формула суммы углов выпуклого n-угольника является мощным инструментом в геометрии, связывающим количество сторон многоугольника с суммой его внутренних углов. Понимание этого принципа существенно расширяет возможности решения геометрических задач.